Untuk gugus data positif x1, x2, …, xn,
rata-rata geometrik adalah akar ke-n dari hasil perkalian unsur-unsur
datanya. Secara matematis dapat dinyatakan dengan formula berikut:
![U = \sqrt[n]{{{x_1}.{x_2}.{x_3} \ldots .{x_n}}}\;{\rm{atau}}\;U = \sqrt[n]{{\prod\limits_{i = 1}^n {{x_i}} }}\;{\rm{atau}}\;{\rm{Log}}(U) = \dfrac{{\Sigma \log ({x_i})\;}}{n} U = \sqrt[n]{{{x_1}.{x_2}.{x_3} \ldots .{x_n}}}\;{\rm{atau}}\;U = \sqrt[n]{{\prod\limits_{i = 1}^n {{x_i}} }}\;{\rm{atau}}\;{\rm{Log}}(U) = \dfrac{{\Sigma \log ({x_i})\;}}{n}](http://l.wordpress.com/latex.php?latex=U+%3D+%5Csqrt%5Bn%5D%7B%7B%7Bx_1%7D.%7Bx_2%7D.%7Bx_3%7D+%5Cldots+.%7Bx_n%7D%7D%7D%5C%3B%7B%5Crm%7Batau%7D%7D%5C%3BU+%3D+%5Csqrt%5Bn%5D%7B%7B%5Cprod%5Climits_%7Bi+%3D+1%7D%5En+%7B%7Bx_i%7D%7D+%7D%7D%5C%3B%7B%5Crm%7Batau%7D%7D%5C%3B%7B%5Crm%7BLog%7D%7D%28U%29+%3D+%5Cdfrac%7B%7B%5CSigma+%5Clog+%28%7Bx_i%7D%29%5C%3B%7D%7D%7Bn%7D&bg=ffffff&fg=000000&s=0)
Keterangan:
U = rata-rata ukur (rata-rata geometrik)
n = banyaknya sampel
Π = Huruf kapital π (pi) yang menyatakan jumlah dari hasil kali unsur-unsur data.
Rata-rata geometrik sering digunakan dalam bisnis dan ekonomi untuk menghitung rata-rata tingkat perubahan, rata-rata tingkat pertumbuhan, atau rasio rata-rata untuk data berurutan tetap atau hampir tetap atau untuk rata-rata kenaikan dalam bentuk persentase.
Contoh 1:
Berapakah rata-rata ukur dari data 2, 4, 8?
Jawab:

atau:
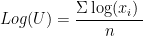
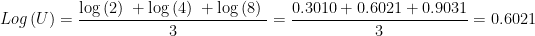
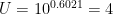
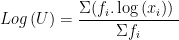
Contoh 2:
Tentukan rata-rata ukur dari tabel distribusi frekuensi pada Contoh 3 di atas!
Jawab:
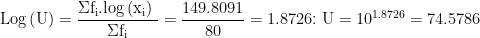
Keterangan:
U = rata-rata ukur (rata-rata geometrik)
n = banyaknya sampel
Π = Huruf kapital π (pi) yang menyatakan jumlah dari hasil kali unsur-unsur data.
Rata-rata geometrik sering digunakan dalam bisnis dan ekonomi untuk menghitung rata-rata tingkat perubahan, rata-rata tingkat pertumbuhan, atau rasio rata-rata untuk data berurutan tetap atau hampir tetap atau untuk rata-rata kenaikan dalam bentuk persentase.
a. Rata-rata ukur untuk data tunggal
Contoh 1:
Berapakah rata-rata ukur dari data 2, 4, 8?
Jawab:
atau:
b. Distribusi Frekuensi:
xi = tanda kelas (nilai tengah)
fi = frekuensi yang sesuai dengan xi
Contoh 2:
Tentukan rata-rata ukur dari tabel distribusi frekuensi pada Contoh 3 di atas!
Jawab:
| Kelas ke- | Nilai Ujian | fi | xi | log xi | fi.log xi |
| 1 | 31 – 40 | 2 | 35.5 | 1.5502 | 3.1005 |
| 2 | 41 – 50 | 3 | 45.5 | 1.6580 | 4.9740 |
| 3 | 51 – 60 | 5 | 55.5 | 1.7443 | 8.7215 |
| 4 | 61 – 70 | 13 | 65.5 | 1.8162 | 23.6111 |
| 5 | 71 – 80 | 24 | 75.5 | 1.8779 | 45.0707 |
| 6 | 81 – 90 | 21 | 85.5 | 1.9320 | 40.5713 |
| 7 | 91 – 100 | 12 | 95.5 | 1.9800 | 23.7600 |
| 8 | Jumlah | 80 | 149.8091 |



0 komentar:
Posting Komentar